T1 求第K小的数(分治)
题目:
用到类似快速排序的分治法。快速排序的思想是把数多次分为三个区间(小于基准数 / 等于基准数 / 大于基准数),再将各个排序好的各个区间拼在一起,就能得到一个排序好的完整数组。
因为分为三个区间后,总数不变,所以直接对原数组进行覆写即可。
快速排序代码:
//qsort (快速排序的核心思想是递归分治)
#include <iostream>
using namespace std;
const int maxx = 100005;
int n,k,a[maxx],b[maxx],c[maxx],d[maxx];
void prework(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
}
void qsort(int l,int r){
if(l>=r){
return;
//len <= 0
}
int t1=0,t2=0,t3=0,mid;
mid = a[(l+r)/2];
for(int i=l;i<=r;i++){
if(a[i]<mid)
b[++t1] = a[i];
else if(a[i]==mid)
c[++t2] = a[i];
else d[++t3] = a[i];
}
for(int i=1;i<=t1;i++)
a[i+l-1] = b[i];
for(int i=1;i<=t2;i++)
a[i+t1+l-1] = c[i];
for(int i=1;i<=t3;i++)
a[i+t1+t2+l-1] = d[i];
qsort(l,l+t1-1);
qsort(l+t1+t2,r);
}
void solve(){
qsort(1,n);
for(int i=1;i<=n;i++) cout<<a[i]<<' ';
}
int main(){
prework();
solve();
}那么要求无序数组第k小的数,会想到进行排序后直接输出对应下标的那个数。然而直接排序复杂度是O(nlogn),大概是10^8这个级别,排序后交也是只有60分,过不了。
自然想到用二分的思想去找 第k小的数。快速排序是以基准数把数组分为两个部分L 和 R,如果要找第k小的数,若L的右边界的数Lr比k大,那第k小的数就在L中,调用函数继续对L划分即可。找到答案的时候是k等于基准数的时候(基准数是在区间里取的,不会出现没有对应的情况)
代码:
#include <iostream>
using namespace std;
const int maxx = 5e6+5;
int n,k,a[maxx],b[maxx],c[maxx],d[maxx],ans;
void prework(){
cin>>n>>k;
for(int i=0;i<n;i++){
cin>>a[i];
}
}
void qsort(int l,int r){
if(l>=r){
ans = a[l];//边界情况更新答案(当l==r时会直接退出
return;
}
int t1=0,t2=0,t3=0,mid;
mid = a[(l+r)/2];
for(int i=l;i<=r;i++){
if(a[i]<mid)
b[++t1] = a[i];
else if(a[i]==mid)
t2++;//c[++t2] = a[i];
else
d[++t3] = a[i];
}
//分成三个区间 L~i~j~R k<=i时 去搜左边的区间
if(l+t1-1>=k){
for(int i=0;i<t1;i++)
a[l+i] = b[i+1];//fill left
qsort(l,l+t1-1);
}
else if(l+t1+t2<=k){
for(int i=0;i<t3;i++)
a[l+t1+t2+i] = d[i+1];
qsort(l+t1+t2,r);
}
else{
ans = mid;//更新答案
return;
}
}
void solve(){
qsort(0,n-1);
cout<<ans;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
prework();
solve();
return 0;
}T2 穿越雷区
题目:

样例:
一道搜索题。
代码:
#include <iostream>
#include <queue>
using namespace std;
struct point{
int x,y,k;
};
int movex[5]={0,1,-1,0,0};
int movey[5]={0,0,0,1,-1};
int n,world[105][105],ans=-1;
bool vis[105][105];
queue<point> a;
bool judge(int x,int y,int nx,int ny){
if(world[nx][ny]==2)
return true;
else if(world[x][y]==world[nx][ny])
return false;
return true;
}
void bfs(){
while(!a.empty()){
point temp = a.front();
int x1=temp.x,y1=temp.y,k1=temp.k;
if(world[x1][y1]==2){
ans = k1;
return;
}
for(int i=1;i<=n;i++){
int nx=x1+movex[i];
int ny=y1+movey[i];
if(nx>=1&&nx<=n&&ny>=1&&ny<=n&&judge(x1,y1,nx,ny)&&vis[nx][ny]==0){
vis[nx][ny]=1;
a.push({nx,ny,k1+1});
}
}
a.pop();
}
}
void prework(){
cin>>n;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
char temp; cin>>temp;
if(temp=='B')
world[i][j]=2;
else if(temp=='A')
world[i][j]=3,vis[i][j]=1,a.push({i,j,0});
else if(temp=='+')
world[i][j]=1;
else
world[i][j]=0;
}
}
}
int main(){
prework();
bfs();
cout<<ans;
return 0;
}T3 KMP字符串匹配 (模板)
题目:

样例:
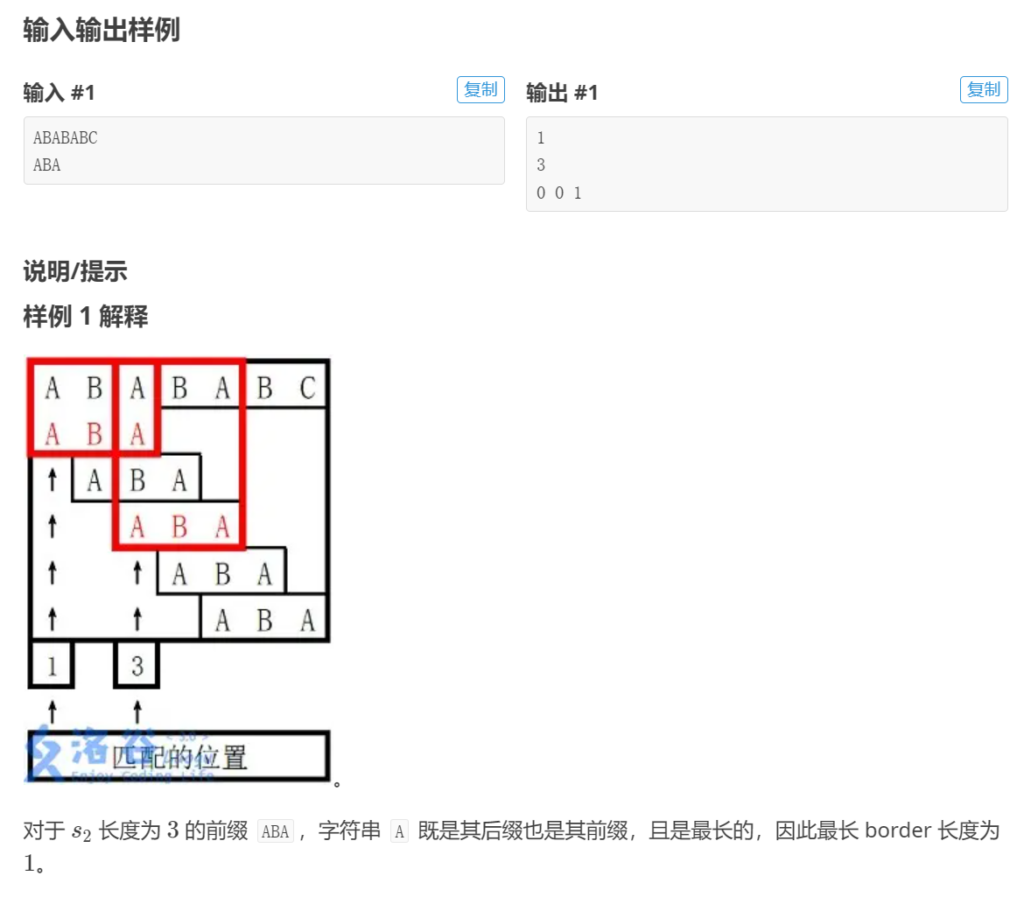
若文本串长度为n,模式串长度为m,则朴素算法复杂度是o(nm),kmp算法其实就是对朴素算法的优化:当匹配过程中出现失配的情况时,可以跳过小于模式串的长度再进行匹配,需要计算记录回文长度的前缀表做到。
代码:
#include <iostream>
#include <cstring>
using namespace std;
const int l = 1000005;
int next_[l],ans,l1,l2;
char t[l],p[l];
string s1,s2;
void trans(){
l1 = s1.length();
l2 = s2.length();
for(int i=0;i<l1;i++){
t[i+1] = s1[i];
if(i<l2) p[i+1] = s2[i];
}
}
void prefix(){
int k=0;
for(int i=2;i<=l2;i++){
while(k>0 && p[k+1]!=p[i])
k = next_[k];
if(p[k+1]==p[i])
k++;
next_[i]=k;//更新next_前缀表
}
}
void kmp(){
int k=0;
for(int i=1;i<=l1;i++){
while(k>0 && p[k+1]!=t[i]){
k = next_[k];
}
if(p[k+1]==t[i])
k++;
if(k==l2){
cout<<i-l2+1<<endl;
k=next_[k];
}
}
}
int main(){
cin>>s1>>s2;
trans();
prefix();
kmp();
for(int i=1;i<=l2;i++)
cout<<next_[i]<<' ';
return 0;
}