T1 查找文献 (dfs bfs模板题)
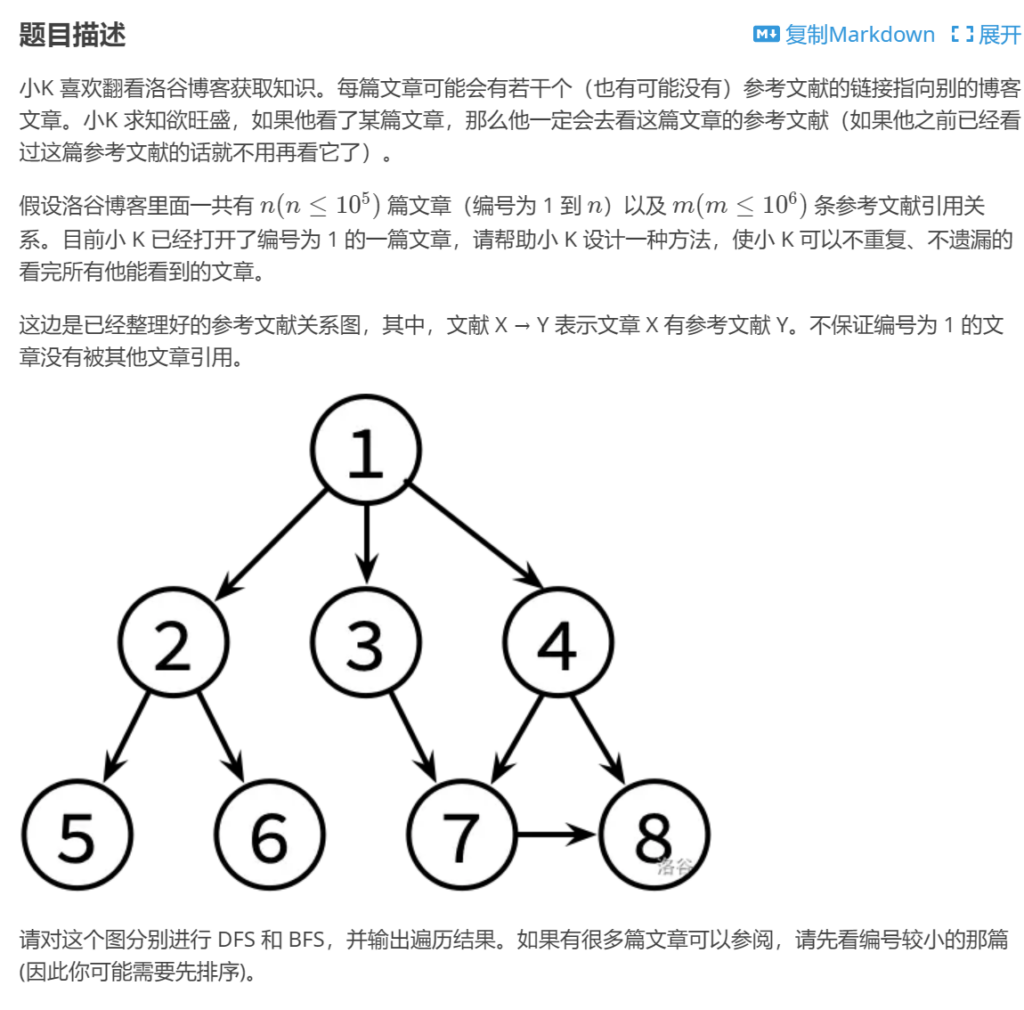
下附代码:
#include <bits/stdc++.h>
using namespace std;
const int maxx=1e6+5;
int n,m;
int vis[maxx];
vector<int> book[maxx];
queue<int> b;
void dfs(int x){
if(vis[x]==1) return;
vis[x]=1;
cout<<x<<' ';
for(int i=0;i<book[x].size();++i){
dfs(book[x][i]);
}
}
void bfs(){
b.push(1);
while(!b.empty()){
int x=b.front();
b.pop();
cout<<x<<' ';
vis[x]=1;
for(int i=0;i<book[x].size();++i){
int next=book[x][i];
if(vis[next]==1) continue;
else{
b.push(next);
vis[next]=1;
}
}
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
int f,e;
cin>>f>>e;
book[f].push_back(e);
}
for(int i=1;i<=n;i++){
sort(book[i].begin(),book[i].end());
}//排序n种资料
dfs(1);
cout<<endl;
memset(vis,0,sizeof(vis));
bfs();
return 0;
}T2 Floyd(最短路n^3模板题)

floyd比较短,本质上是一种dp算法。时间复杂度为 n^3,n<10^3内的数据可以用。floyd适用性也很高,遍历所有点所以可以做到一些生成树算法的功能。
下附代码:
#include <iostream>
#include <cstring>
using namespace std;
const long long int mod = 998244354;
const long long int INF=25e13+500;
int n,m;
long long int ans;
long long int map[505][505];
int main(){
for(int i=1;i<=503;i++)
for(int l=1;l<=503;l++){
if(i==l) map[i][l]=0;
else map[i][l]=INF;
}
cin>>n>>m;
for(int i=1;i<=m;i++){
int s,e,v;
cin>>s>>e>>v;
if(map[s][e]!=0&&map[s][e]>v){
map[s][e]=v;
map[e][s]=v;
}
//无向图。
}
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int l=1;l<=n;l++){
if(i==l) continue;
if(map[k][l]<INF&&map[i][k]<INF&&map[i][l]>(map[k][l]+map[i][k]))
map[i][l]=(map[k][l]+map[i][k]);
}
}
}
for(int i=1;i<=n;i++){
ans=0;
for(int l=1;l<=n;l++){
ans+=map[i][l];
ans%=mod;
}
cout<<ans%mod<<endl;
}
return 0;
}T3 单源最短路径(标准版)
用dijkstra时要用堆来优化缩边过程的选点步骤,可以用优先队列来存放到各点的估计值。

各种存图方式,代码用了vector数组进行存图

下附代码:
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
const int inf=2e9+5;
struct point{
int end,len;
bool operator < (const point a) const{
return len < a.len;
}//重载运算符
bool operator > (const point a) const{
return len > a.len;
}
};
int n,m,st,cnt,now;
bool book[100005];
vector <point> a[100005];//最多1e5个点
priority_queue <point, vector<point>,greater<point> > dis;
int ans[100005];//存答案的数组。
int main(){
cin>>n>>m>>st;
for(int i=1;i<=100005;i++){
ans[i]=inf;
}
ans[st]=0;
for(int i=1;i<=m;i++){
int s,e,v;
cin>>s>>e>>v;
a[s].push_back({e,v});
}//vector存图
dis.push({st,0});//存入起点
while(!dis.empty()){
point temp=dis.top();
dis.pop();
now=temp.end;
//因为确定值不能重复更新(优先队列内仍可能存在
//所以要加一个判断。
if(!book[now]){
book[now]=true;
for(int i=0;i<a[now].size();i++){
//遍历所有边 vector下标从0开始
point x=a[now][i];
int to=x.end;
int v=x.len;
//dijkstra核心代码
if(ans[to]>ans[now]+v){
ans[to]=ans[now]+v;
//dijkstra核心代码
if(!book[to]){
//减少判断次数,去掉不影响算法正确性。
dis.push({to,ans[to]});
}
}
}
}
}
for(int i=1;i<=n;i++){
cout<<ans[i]<<' ';
}
return 0;
}