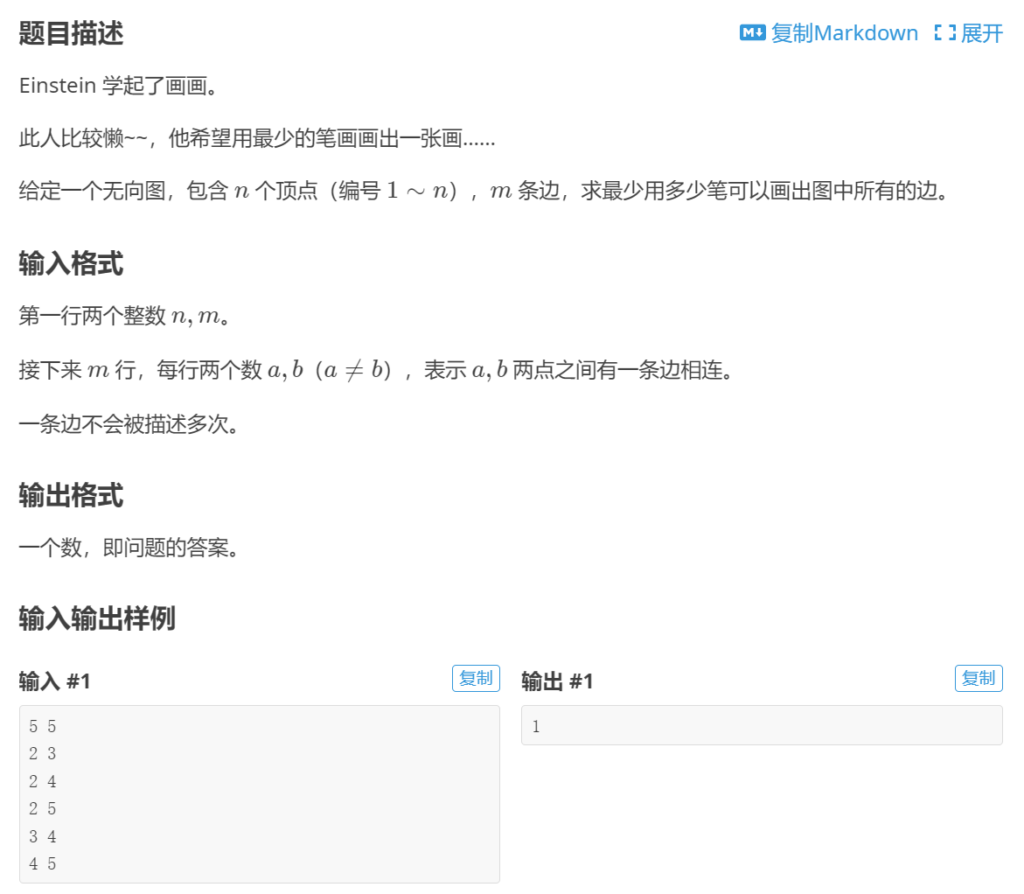
T1 Einstein学画画
是一题(一笔画)欧拉路的模板。欧拉路 是指若从起点到终点的路径恰经过图中每条边一次,则该路径成为欧拉路。存在欧拉路的条件是:图是联通的,且有0个或2个奇点(出入度为奇数的点)。欧拉路一定是从一个奇点开始,到另一个奇点结束,所以有两个奇点的时候能一笔画完。
若每多出两个奇点,画的次数就会+1,所以答案就是 奇点的个数 / 2。
//当一个无向图的奇点数为0或者2的时候
//可以不重边的走完所有点
//奇点为度为奇数的点
//所以一幅图要(奇点数/2)笔画完
#include <iostream>
using namespace std;
int du[1005];//统计一个点的度数
int main(){
int n,m; cin>>n>>m;
for(int i=1;i<=m;i++){
int s,e;
cin>>s>>e;
du[s]++;
du[e]++;
//无向图,所以出入度相等
}
int ans=0;
for(int i=1;i<=n;i++)
if(du[i]%2)
ans++;
if(ans==0) cout<<"1";//小特判
else cout<<ans/2;
return 0;
}
T2 合根植物(并查集)
是一道并查集的板子题,需要路径压缩。

#include <iostream>
using namespace std;
int n,m,k;
int f[1000005];
void init(){
for(int i=1;i<=1000000;i++)
f[i]=i;
return;
}//初始化是必须的
int getf(int v){
if(f[v]==v)
return v;//查找根节点
else{
f[v]=getf(f[v]);
return f[v];//路径压缩
}
}//查找
void merge(int a,int b){
int b1,b2;
b1=getf(a);
b2=getf(b);
if(b1!=b2){
f[b2]=b1;
//左靠原则
}
return;
}//合并
int main(){
cin>>n>>m>>k;
//n为行数,m为列数
init();
for(int i=1;i<=k;i++){
int x,y;
cin>>x>>y;
merge(x,y);
}
int sum=0;
int tot=n*m;
for(int i=1;i<=tot;i++){
if(f[i]==i)
sum++;
}
cout<<sum;
return 0;
}T3 奶酪
题目可以用dfs进行n^2的遍历,通过两点球心距离和两球半径之和的孰大孰小判断两球是相交,相切还是相离。

#include <iostream>
#include <cmath>
#include <cstring>
#include <stdio.h>
using namespace std;
long long int t,n,h,r;
bool vis[1005],found;
struct ball{
int x,y,z;
}p[1004];
bool link(ball a,ball b){
long long int dis=(pow(a.x-b.x,2)+pow(a.y-b.y,2)+pow(a.z-b.z,2));
//两点距离的平方与2r的平方对比
if(dis>4*r*r)
return false;
else return true;//如果相交
}
void dfs(int a){
if(found==true) return;
if(p[a].z+r>=h){
found=true;
return;
}
for(int i=1;i<=n;i++){
if(vis[i]==true) continue;
else{
if(link(p[a],p[i])){
vis[i]=true;
dfs(i);
}//如果相交
}
}
}
int main(){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
cin>>t;
while(t--){
found = false;
memset(vis,false,sizeof(vis));
//初始化
cin>>n>>h>>r;
for(int i=1;i<=n;i++){
cin>>p[i].x>>p[i].y>>p[i].z;
}
for(int i=1;i<=n;i++){
if(p[i].z<=r){
dfs(i);
//如果和底边相交或相切
}
}
if(found==true) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
return 0;
}T4 灾后重建(最短路)
用了动态规划的思想,是一道很好的练习floyd的题。

#include <iostream>
#include <stdio.h>
using namespace std;
const int inf=1e9+5;
int map[205][205];
int n,m,q,t[205];
int st,ed,v;//临时变量
void init(){
for(int i=0;i<n;i++)
for(int l=0;l<n;l++){
map[i][l]=inf;
}
for(int i=0;i<n;i++) map[i][i]=0;
}//初始化
void updata(int x){
for(int i=0;i<n;i++){
for(int l=0;l<n;l++){
map[i][l]=min(map[i][l], map[i][x]+map[x][l]);
}
}
}
int main(){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
cin>>n>>m;
init();
for(int i=0;i<n;i++) cin>>t[i];
for(int i=0;i<m;i++){
cin>>st>>ed>>v;
map[st][ed]=v;
map[ed][st]=v;
//存图
}
cin>>q;
int cur=0;
while(q--){
cin>>st>>ed>>v;
while(t[cur]<=v&&cur<n){
updata(cur);
cur++;//时间是逐渐变大的,所以已经做过中转的村庄不会再用到
}
if(t[st]>v||t[ed]>v||map[st][ed]==inf) cout<<"-1"<<endl;
else cout<<map[st][ed]<<endl;
}
return 0;
}T5 聪明的猴子
生成树的模板题。

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
struct edge{
int s,e;
long long int v;
}p[1000005];
int f[1005];
int x[1005],y[1005];
int M,mk[505],n;
int ans;
int cnt;
int getf(int x){
if(f[x]==x) return x;
else{
f[x]=getf(f[x]);
return f[x];
}
}
bool merge(int x,int y){
int x1,y1;
x1=getf(x);
y1=getf(y);
if(x1!=y1){
f[x1]=y1;
return true;
}
return false;//已经联通
}
void init(){
for(int i=1;i<=n;i++){
f[i]=i;
}
return;
}
long long int len(int x1,int y1,int x2,int y2){
return (x1-x2)*(x1-x2)+(y1-y2)*(y1-y2);//返回距离的平方
}
bool cmp(edge a,edge b){
return a.v<b.v;
}
int main(){
cin>>M;
for(int i=1;i<=M;i++){
int aa; cin>>aa;
mk[i]=aa*aa;
}
sort(mk+1,mk+1+M);
cin>>n;
init();
for(int i=1;i<=n;i++){
cin>>x[i]>>y[i];
}//读入数据
for(int i=1;i<=n;i++){
for(int l=i+1;l<=n;l++){
long long int lens;
lens=len(x[i],y[i],x[l],y[l]);
cnt++;
p[cnt].s=i;
p[cnt].e=l;
p[cnt].v=lens;
//读入所有边
}
}
int time=n*(n-1)/2;
sort(p+1,p+1+time,cmp);//对time条边进行排序
cnt=0;
long long int max=0;
for(int i=1;i<=time;i++){
if(merge(p[i].s,p[i].e)){
cnt++;
max=p[i].v;
}
if(cnt==time-1) break;
}
for(int i=M;i>=1;i--){
if(mk[i]>=max) ans++;
else break;
}
cout<<ans;
return 0;
}