T1 疯狂的采药
题目:

是经典的01背包问题,在博客另一处有介绍,推出 状态转移方程即可。
代码如下。
#include <iostream>
using namespace std;
long long int T,n;
long long int t[10005],w[10005];
long long int dp[10000005];
int main(){
cin>>T>>n;
for(int i=1;i<=n;i++)
cin>>t[i]>>w[i];
for(int i=1;i<=n;i++){
for(int l=1;l<=T;l++){
if(l>=t[i])
dp[l]=max(dp[l],dp[l-t[i]]+w[i]);
}
}
cout<<dp[T];
return 0;
}T2 摆花
题目:
计数dp
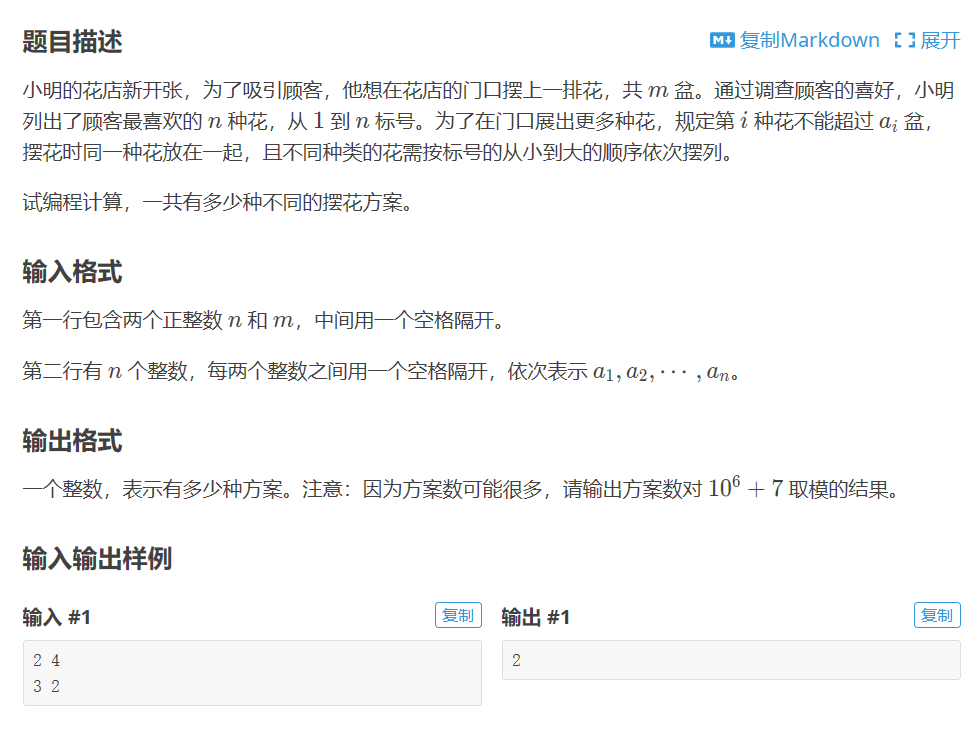
用填表法的思想可以得出更新dp数组的式子。
#include <iostream>
using namespace std;
const long long int x=1000007;
long long int n,m,a[104],dp[105][105];
//dp[i][j]记录有i种花,要摆j盆时的摆法。
int main(){
dp[0][0]=1;//一种花都没有的话是一种情况。
cin>>n>>m;
for(long long int i=1;i<=n;i++)
cin>>a[i];
for(long long int i=1;i<=n;i++){
for(long long int l=0;l<=m;l++){
for(long long int p=0;p<=min(l,a[i]);p++){
dp[i][l]=(dp[i][l]+dp[i-1][l-p])%x;//每次都取模。
}
}
}
cout<<dp[n][m];
return 0;
}T3 樱花
题目:
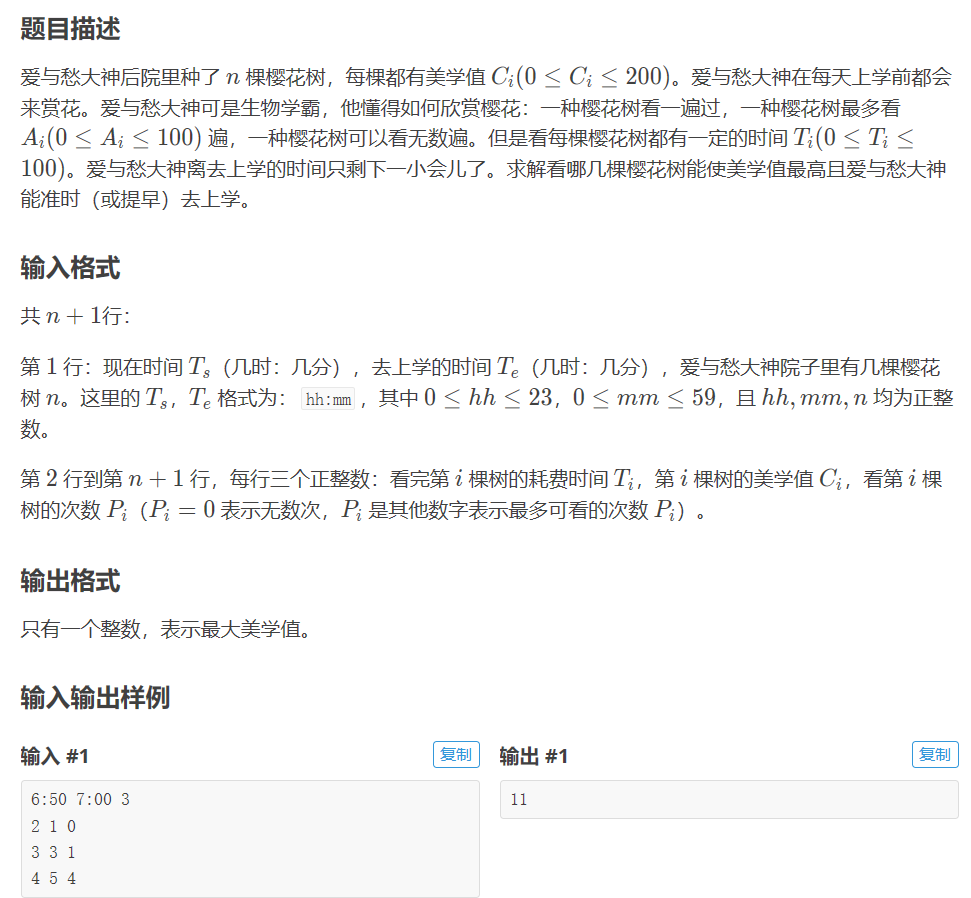
看题可以知道有些美学值是可以拿很多甚至无限次的,所以这是一个多重背包问题,可以用二进制优化将复杂度由O(n^3)优化至O(n^2 logn)
可以把没有次数限制的美学值次数设成一个比较大的数。
代码如下。
#include <bits/stdc++.h>
using namespace std;
int N,V;
int v[100000005],w[100000006],dp[100000005];
long long int hs,ms,he,me;
int main(){
scanf("%lld:%lld %lld:%lld %lld",&hs,&ms,&he,&me,&N);
he-=hs;
if(me-ms<0)
me=me-ms+60,he--,me+=he*60;
else me = me - ms + he * 60;
V=me;
int count=0;
//分成2^0(1),2^1(2),2^2(4),2^3(8)...余数组。
//O(n^3)->O(n^2logS)
for(int i=1;i<=N;++i){
int z,x,c;
cin>>z>>x>>c;
if(c==0) c=9999999;
for(int k=1;k<=c;k*=2){
count++;
v[count]=z*k;
w[count]=x*k;
c-=k;
}
if(c>0){
count++;
v[count]=z*c;
w[count]=x*c;
}
}
for(int i=1;i<=count;++i){
for(int k=V;k>=0;k--){
if(k>=v[i])
dp[k]=max(dp[k],dp[k-v[i]]+w[i]);
}
}
cout<<dp[V];
return 0;
}T4 金明的预算方案
题目:

这题存附件数据技巧是开二维数组cost[x][y],x为第x件物品,当y为0时为这件物品本身,y为1时为第x件物品的附件1,y为2时为第x件物品的附件2。
然后每次选择有五种情况,
①只买主件
②买主件+附件1
③买主件+附件2
④买主件+附件1+附件2
⑤不买主件。
除了1和5冲突外,其他四个都能判断后更新新的dp值,顺序任意,枚举这五种情况,填表即可。
代码如下。
#include <iostream>
#include <cstring>
using namespace std;
int m,n;
int dp[70][40000];
int cost[70][5],imp[70][5];
int main(){
cin>>m>>n;
int c,im,f;
for(int i=1;i<=n;i++){
cin>>c>>im>>f;
if(!f){
cost[i][0]=c;
imp[i][0]=im;
}
else{
if(!cost[f][1]){
cost[f][1]=c;
imp[f][1]=im;
}
else{
cost[f][2]=c;
imp[f][2]=im;
}
}
}
memset(dp,0,sizeof(dp));
for(int i=1;i<=n;i++){
for(int l=1;l<=m;l++){
if(l-cost[i][0]>=0){
dp[i][l]=max(dp[i-1][l],dp[i-1][l-cost[i][0]]+cost[i][0]*imp[i][0]);
if(l-cost[i][0]-cost[i][1]>=0){
dp[i][l]=max(dp[i][l],dp[i-1][l-cost[i][0]-cost[i][1]]+cost[i][0]*imp[i][0]+cost[i][1]*imp[i][1]);
}
if(l-cost[i][0]-cost[i][2]>=0){
dp[i][l]=max(dp[i][l],dp[i-1][l-cost[i][0]-cost[i][2]]+cost[i][0]*imp[i][0]+cost[i][2]*imp[i][2]);
}
if(l-cost[i][0]-cost[i][1]-cost[i][2]>=0){
dp[i][l]=max(dp[i][l],dp[i-1][l-cost[i][0]-cost[i][1]-cost[i][2]]+cost[i][0]*imp[i][0]+cost[i][1]*imp[i][1]+cost[i][2]*imp[i][2]);
}
}
else
dp[i][l]=dp[i-1][l];
}
}
cout<<dp[n][m];
return 0;
}总结:
记忆化搜索>dp?)。
代码写的好丑呀。(不是什么大问题就是)