顺序查找时间复杂度为O(n),在数据量为1e8左右时计算机能在1s内处理完毕,但数据量为1e9及以上的时候,仍采用顺序查找对于计算机就比较吃力了,效率相当低。
二分查找有个很重要的特点,就是不会查找数列的全部元素,而查找的数据量其实正好符合元素的对数,正常情况下每次查找的元素都在一半一半地减少。在最坏的情况和一般情况下都比顺序查找要快。
使用二分查找的条件:
查找的序列必须要是单调的。
(假如考拉猫搬着刚借的1e5本书走出图书馆,两侧的门突然响了(bushi)
T1 二分查找
Tag:基础 二分查找。
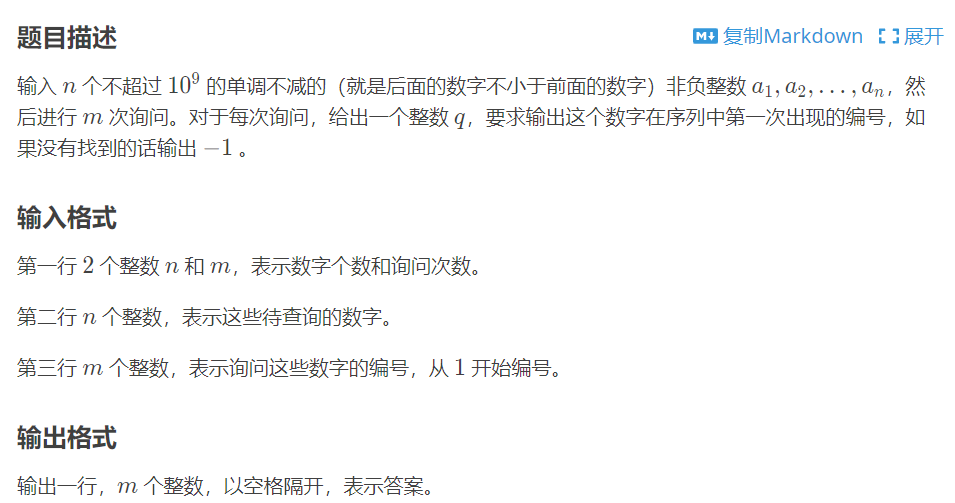
(思路呢)
代码如下。
#include <iostream>
using namespace std;
int n,n_q;
long long int q;
int main(){
cin>>n>>n_q;
long long int num[n+5];
for(int i=1;i<=n;i++) cin>>num[i];//输入数据。
while(n_q--){
cin>>q;//输入询问的数。
long long int l=0,r=n+1,mid;
while(l+1!=r){//左边界是询问数的编号-1
mid=(l+r)/2;//更新数据。
if(num[mid]>=q){
r=mid;
}
else{
l=mid;
}
}//找边界。
if(num[l+1]==q){
cout<<l+1<<' ';
}//如果找到了 输出左边界加一l+1。
else cout<<"-1 ";
//找不到 输出-1。
}
return 0;
}有时候会遇到 最大值的最小 或者 最小值的最大 问题,直接去做不好做,但是检查一个答案可不可行是比较简单的。然后用二分的思想 不断缩小答案的区间,最后获得可行答案的最大值。
T2 进击的奶牛
tag:二分答案 可行最大值。
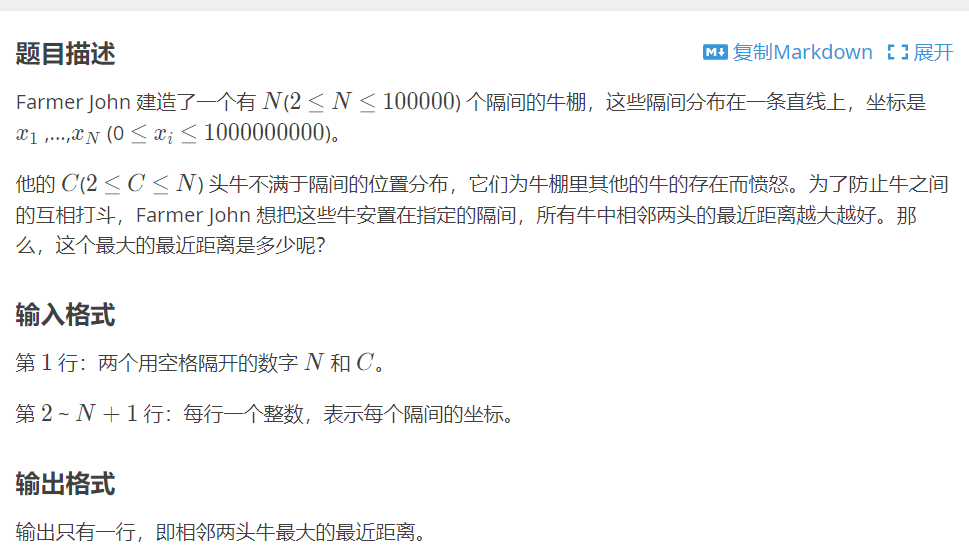
用二分答案的思想去做,需要写检查函数。对于这道题,要将牛从左到右进行安置,直到所有牛棚被安排完或者所有牛被安置完。
代码如下。
#include <iostream>
#include <algorithm>
using namespace std;
int N,C;//N是牛棚的数量,C是牛的数量。
long long int x[100005];//是牛棚的坐标。
bool check(long long int ans){//检查函数将牛从左至右安置。
long long int start=x[1],end,cow=C-1;
for(int i=2;i<=N&&cow!=0;i++){
end=x[i];
//如果两个牛棚间隔大于答案的值,安置好了一头牛。
if(end-start>=ans){
start = end;//更新左边的牛棚。
cow--;//需要安置的牛-1。
}
}
if(cow<=0) return true;//如果所有的牛都安置好了,这个答案可行。
else return false;
}
int main(){
cin>>N>>C;//输入数据。
for(int i=1;i<=N;i++){
cin>>x[i];
}
sort(x+1,x+N+1);//不要忘记排序。
//开始写二分搜索答案。
long long int l=0,r=1e10+5,mid;
while(l<=r){
mid=(l+r)/2;
//如果答案可行,把左边界的值右移。
if(check(mid)){
l=mid+1;
}
else
r=mid-1;
}
cout<<l-1;//输出答案。
return 0;
}坑点是不要忘记排序,还有检查函数循环的结束条件。
T3 一元三次仿鲿求解。
tag:二分答案 简单 枚举。

这题注意到根的范围比较小,且根于根之差的绝对值大于等于1,所以可以枚举两百个点找根。
活用题面与提示,找够三个点后退出循环,然后输出答案。
获得精确到小数点后两位的答案,有两种方法
①一种是L,R作差的值精确到0.001时返回答案。
②一种是限定次数的浮点二分。(机宝hso)
代码如下。
#include <iostream>
#include <cmath>
using namespace std;
double a,b,c,d;
double temp;
double ans[4];//记录答案的数组(其实可以不要)
int cnt=1;
double f(double x){
return (a*pow(x,3)+b*pow(x,2)+c*x+d);
}//计算函数值的函数。
bool root(double l,double r){
if(f(l)*f(r)<0) return true;
else return false;
}//非常简单的检查函数。
int main(){
cin>>a>>b>>c>>d;
for(int i=-100;i<100;i++){//枚举200个点。
if(cnt==4) break;//存够答案就可以了。
if(f(i)==0){
ans[cnt++]=i;
continue;
}
if(root(i,i+1)){//初步判断有没有根。
double l=i,r=i+1,mid;
int tot=1;//计数器。
while(++tot<60){//限定次数的浮点二分。
mid = (l+r)/2;
if(root(l,mid)){
r=mid;
}
else l=mid;
temp=mid;
}
ans[cnt++]=temp;
}
}
printf("%.2f %.2f %.2f",ans[1],ans[2],ans[3]);
return 0;
}T4 锯树
tag:二分答案 可行最大值

代码如下。
#include <iostream>
using namespace std;
const int N=1e6+5;
int n;//n为树木的数量。
long long int tree[N],need;//数的高度 和 需要的木头长度。
bool check(long long int x){
long long int sum=0;//砍下的木材长度计数。
for(int i=1;i<=n;i++)
if(x<tree[i]){//如果木头能锯到树。
sum+=tree[i]-x;//长度-锯子高度。
}
if(sum>=need) return true;//如果锯够了。
return false;
}
int main(){
cin>>n>>need;
for(int i=1;i<=n;i++){
cin>>tree[i];
}//输入数据。
long long int l=0,r=2e9+5,mid;
//要求锯最少的树满足条件。(即求满足条件的最大值。
while(l<=r){
mid=(l+r)/2;
if(check(mid)){//如果答案可行,找更高的值。
l=mid+1;
}
else r=mid-1;
}
cout<<l-1;
return 0;
}T5 跳石头
tag:二分答案 边界最大值。

坑点:有可能要把第一颗或者最后一颗石头移走的情况,所以起点要设置成0,然后要把终点存入rock数组中,这样才能对最后一颗石头进行判定。
#include <iostream>
using namespace std;
const int N=5e5+5;
int l,n,m;// l是长度,n是岩石个数,m是可移走的石头数。
int rock[N];//记录石头 距离起点的 长度。
bool check(int x){
int cnt=0,start=0,end;
for(int i=1;i<=n+1;i++){
end=rock[i];//更新下一个石头的值。
if(end-start<x){//如果两个石头距离小于检查的距离。
cnt++;//说明要移走一个石头。
}
else //否则更新上一个石头的值。
start=end;
}
if(cnt<=m) return true;
return false;
}
int main(){
cin>>l>>n>>m;
for(int i=1;i<=n;i++)
cin>>rock[i];
rock[n+1]=l;//坑点 最后一个石头也要进行判断。
//所以要把他存入rock数组里。
int l=0,r=1e9+5,mid;//二分。
while(l<=r){
mid=(l+r)/2;
if(check(mid)){//如果答案可行。
l=mid+1;//更新左边界的值。
}
else r=mid-1;//不可行更新右边界的值。
}
cout<<r;//输出r。
return 0;
}T6 三分法。
tag:三分模板。
这道题听说是典型的三分模板,用小学思维求导二分也行,但对于一些复杂函数求导并不是那么的方便。
这道题的思路是:在[L,R]上取两个三等分点记为 x=i 和 x=j ,肯定是f(x)更大的的数更靠近拐点。
所以为了让范围更接近拐点,可以让没那么接近的那个点为新的边界,不断缩小范围直到满足精确度
的条件。

坑点:三等分点不是(l+r)*(1/3)呜呜。
代码如下。
#include <iostream>
#include <cmath>//需要用到指数运算。
using namespace std;
int n;//函数有n+1项。
double l,r,ll,rr,cut;//ll,rr为左右三等分点
//cut为[L,R]三等分后每一段的长度。
//函数次数为6到13,所以定义一个数组存各项系数。
double a[20];
//计算并返回函数值的函数。
double f(double x){
double sum=0;
for(int i=0;i<=n;i++)
sum+=a[i]*pow(x,i);
return sum;
}
int main(){
cin>>n>>l>>r;
//注意是从次数大的系数开始输入。
for(int i=n;i>=0;i--) cin>>a[i];
while(abs(l-r)>0.00001){
cut = (r-l)/3.0;
ll=l+cut;//加三分之一长度。
rr=r-cut;//减三分之一长度。
if(f(ll)>=f(rr))//如果左边的点更靠近。
r=rr;//更新右边界。
else l=ll;//否则更新左边界。
}
printf("%.5lf",(l+r)/2.0);
return 0;
}大概就是这样?
好难哦。
存在的问题:
①二分答案的题写少了,检查函数写的很慢。
②其实对答案该怎么保存还是不太熟悉的(基本都是在调试的时候直接输出边界附近的数)
好累啊我要玩东方去了(摆。