01背包——>拿或不拿的问题。
问题:有N件体积为v,价值为w的物品。和一个体积为V的背包,求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
可以先定义一个二维数组dp[i][j]表示在第i件物品,体积为j的时候的总价值。
可以推出状态转移方程:
dp[i][j]=max ( dp[i-1][j] , dp[i-1][j-v[i]]+w[i])
由此可知用双重循环遍历所有物品和体积,可以推出答案即dp[N][V]的值。
代码如下。
//01背包问题。
#include <iostream>
using namespace std;
int N,V;//N件物品,V为背包容量。
int v[1005],w[1005];//v为物品的体积,w为物品的价值。
int dp[1005][1005];//dp[i][j]为价值量 i为第i件物品,j为背包剩余的容量。
//!!dp[0][0-1005]为0(有可能会有测试点测0,0)
int main(){
cin>>N>>V;
//存储数据。
for(int i=1;i<=N;i++){
cin>>v[i]>>w[i];
}
//状态转移方程:
for(int i=1;i<=N;i++){
for(int k=1;k<=V;k++){
if(k<v[i])//如果第i个物品放不下。
dp[i][k]=dp[i-1][k];//这个物品不拿。
else
dp[i][k]=max(dp[i-1][k],dp[i-1][k-v[i]]+w[i]);//不拿或拿。
}
}
cout<<dp[N][V];//输出答案。
}但是可以发现运用二维数组记录答案即浪费空间也浪费时间,有10000件以上物品的时候很容易超时。
所以可以把dp二维数组压缩成一维数组优化,即滚动数组优化。
打表可以发现,在递推的过程中只是用到了和上一层的数据。
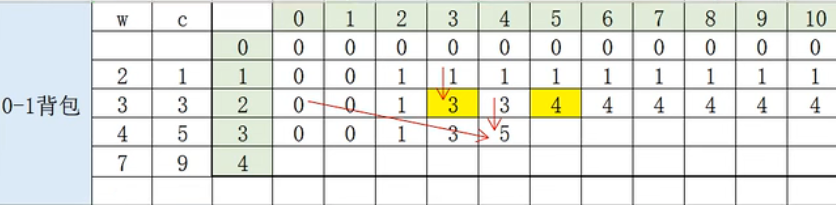
所以可以数组下标只记录背包的体积 dp[V],并通过不断的覆盖避免了记录大量无用数据的问题。(?)
(坑点)但是要注意的是,用一维数组滚动要避免可能要用的数据过早被覆盖的问题,表中正向体积V是不断增大的,小背包能装的东西大背包也一定能装,反过来就不一定了,所以要逆向去更新覆盖数组中的数据。
代码如下。
//01背包问题。
#include <iostream>
using namespace std;
int N,V;//N件物品,V为背包容量。
int v[1005],w[1005];//v为物品的体积,w为物品的价值。
int dp[1005];//dp[j]为体积为J时能装的价值量。 j为背包剩余的容量。
//!!dp[0][0-1005]为0(有可能会有测试点测0,0)
int main(){
cin>>N>>V;
//存储数据。
for(int i=1;i<=N;i++){
cin>>v[i]>>w[i];
}
//状态转移方程:
for(int i=1;i<=N;i++){
for(int k=1;k<=V;k++){
if(k<v[i])//如果第i个物品放不下。
dp[i][k]=dp[i-1][k];//这个物品不拿。
else
dp[i][k]=max(dp[i-1][k],dp[i-1][k-v[i]]+w[i]);//不拿或拿。
}
}
cout<<dp[N][V];//输出答案。
}完全背包问题(每件物品都有无限件)
问题:有N种体积为v,价值为w的物品。和一个体积为V的背包,每种物品的数量是无限的,求解将怎样将物品分配入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
因为物品无限所以可以变成0/1/2/3…背包问题(?)
诶嘿,设k为取用一种物品的数量,观察原来的状态转移方程,发现可以在原来的基础上做一些小更改。
dp[i][j]=max ( dp[i-1][j] , dp[i-1][j-v[i]]+w[i])
↓↓↓ ↓↓↓
dp[i][j]=max ( dp[i-1][j] , dp[i-1][j-k*v[i]]+k*w[i])
再用滚动数组优化
dp[j]=max ( dp[j] , dp[j-k*v[i]]+k*w[i])
代码如下:
#include <iostream>
using namespace std;
int w[1005],v[1005],dp[1005];
int main(){
int N,V; cin>>N>>V;//N为物品数量,V为背包体积。
for(int i=1;i<=N;i++)
cin>>v[i]>>w[i];
for(int i=1;i<=N;i++){
for(int j = V;j>=0;k++){
for(int k=0;k<=j/v[i];k++)
dp[j] = max(dp[j],dp[j-k*v[i]]+k*w[i]);//不用判断能不能装得下了。
}
}
cout<<dp[V];
return 0;
}但是因为用到了三重循环,所以这是非常土的方法。
可以再打个表看看。

可以发现新的数据是来自于上一行数据和新产生的数据。
在01背包的滚动数组里,新的数据是来自于上一行和上一行的旧数据得出的。
所以在完全背包可以无需给取用的物品计数,直到拿不下为止,从0开始,顺向去求解dp[V]的值。
代码如下。
#include <iostream>
using namespace std;
int w[1005],v[1005],dp[1005];
int main(){
int N,V; cin>>N>>V;//N为物品数量,V为背包体积。
for(int i=1;i<=N;i++)
cin>>v[i]>>w[i];
for(int i=1;i<=N;i++){
for(int k = 1;k<=V;k++){//顺向,要用到新数据。
if(k>=v[i])//可以从v[i]开始省掉一次判断(优化。
dp[k] = max(dp[k],dp[k-v[i]]+w[i]);
}
}
cout<<dp[V];
return 0;
}非常的奇妙。
多重背包问题(要变成01背包问题吗?)
直接拆成01背包问题是可以的,也可以多加一层循环。
for(int l=0;l<=s[i]&&l*v[i]<=k;l++)
还有感觉非常帅气,短小精悍的saber简化代码。
#include <bits/stdc++.h>
using namespace std;
int dp[1005],n,t,v,w,s;
main()
{
cin>>n>>t;
while(n--)
{
cin>>w>>v>>s;
while(s--)
for(int j=t;j>=w;j--)
dp[j]=max(dp[j],dp[j-w]+v);
}
cout<<dp[t];
}